
- CHI SQUARE DISTRIBUTION DEGREES OF FREEDOM GENERATOR
- CHI SQUARE DISTRIBUTION DEGREES OF FREEDOM SERIES
(1) is distributed as with degrees of freedom. Test statistics based on the chi-square distribution are always greater than or equal to zero. If have normal independent distributions with mean 0 and variance 1, then. For \(df > 90\), the curve approximates the normal distribution. The chi-square distribution curve is skewed to the right, and its shape depends on the degrees of freedom \(df\). The key characteristics of the chi-square distribution also depend directly on the degrees of freedom. The random variable in the chi-square distribution is the sum of squares of df standard normal variables, which must be independent. When the number of degrees of freedom n tends towards infinity, the chi-square distribution tends (relatively slowly) towards a normal distribution. Everything youll need for your studies in one place for Chi-Square. The shape of a chi-square distribution depends on its degrees of freedom, k. The mean of a chi-square distribution is the degrees of freedom: 2 k. Compare the blue curve to the orange curve with 4 degrees of freedom. But, it has a longer tail to the right than a normal distribution and is not symmetric. In all cases, a chi-square test with k 32 bins was applied to test for normally distributed data.

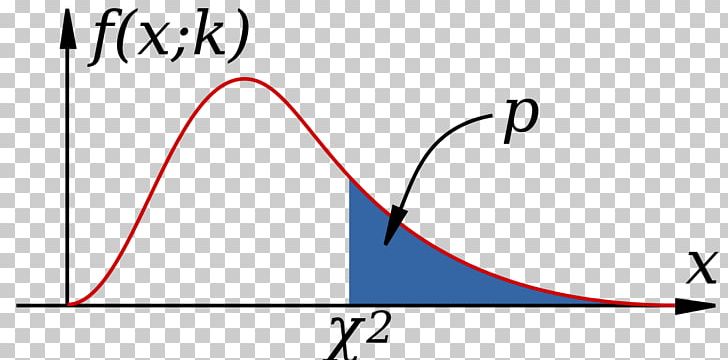
These problem categories include primarily (i) whether a data set fits a particular distribution, (ii) whether the distributions of two populations are the same, (iii) whether two events might be independent, and (iv) whether there is a different variability than expected within a population.Īn important parameter in a chi-square distribution is the degrees of freedom \(df\) in a given problem. A chi-square distribution is a continuous probability distribution. Figure 1: Chi-Square distribution with different degrees of freedom You can see that the blue curve with 8 degrees of freedom is somewhat similar to a normal curve (the familiar bell curve). The chi-square test is defined for the hypothesis: Chi-Square Test Example We generated 1,000 random numbers for normal, double exponential, t with 3 degrees of freedom, and lognormal distributions.
CHI SQUARE DISTRIBUTION DEGREES OF FREEDOM SERIES
The chi-square distribution is a useful tool for assessment in a series of problem categories. Chi-Square Independence Test - What Is It The chi-square independence test evaluates if two categorical variables are related in some population. The mean, \(\mu\), is located just to the right of the peak.I've asked a follow-up question at chi-squared goodness-of-fit: effect size and power.\). I have a large sample size but since I'm unsure of its relation to p-value (increased sampling reduces errors but significance value represents a ratio in the types of errors) I think I'll just stick with the standard value 0.05.Įdit: actual questions italicized above, and enumerated below: It is used to describe the distribution of a sum of squared random. The chi-squared distribution is implemented in the Wolfram Language as ChiSquareDistribution n. The degrees of freedom in a chi square distribution is also its mean. For example, if you have taken 10 samples from the normal distribution, then df 10. Select a confidence significance value $c$ such that $p > c$ signifies the distribution is probably uniform. A chi-square distribution is a continuous distribution with k degrees of freedom. The Chi-Square Distribution The degrees of freedom (k) are equal to the number of samples being summed. follows a Fisher distribution with n 1 and n 2 degrees of freedom. If two random variables X 1 and X 2 follow a chi-square distribution with, respectively, n 1 and n 2 degrees of freedom, then the random variable. Let X1andX2be independent random variables having the chi-squaredistributions with degrees of freedomn1andn2, respectively.By the transformation theorem, the p.d.f.
CHI SQUARE DISTRIBUTION DEGREES OF FREEDOM GENERATOR
I have a third party random number generator with a period approximately greater than $63*(2^ - 1$ degrees of freedom.Īs far as I can tell, no chi-squared distribution exists for that many degrees of freedom. The chi-square distribution is a continuous probability distribution with the values ranging from 0 to (infinity) in the positive direction. The chi-square distribution is a particular case of the gamma distribution.


 0 kommentar(er)
0 kommentar(er)
